Autor: dr Adam Jarmuła, Instytut Biologii Doświadczalnej im. M. Nenckiego PAN
Dynamika molekularna (DM) jest metodą symulacji zależnego od czasu zachowania się modelowego układu molekuł (atomy, cząsteczki). Atomy są traktowane jako punkty materialne obdarzone ładunkiem i połączone ze sobą wiązaniami. Ewolucja w czasie układu wzajemnie oddziałujących atomów jest opisywana dzięki numerycznemu całkowaniu ich równań ruchu przy zastosowaniu periodycznych warunków brzegowych (Rysunek 1) odpowiednich z uwagi na symetrię badanego układu.
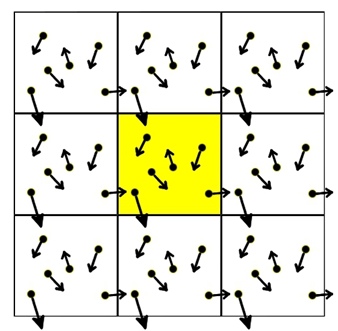
Rysunek 1. Periodyczne warunki brzegowe
Pokolorowana na żółto komórka reprezentuje właściwy symulowany układ, pozostałe komórki są jej dokładnymi kopiami, co oznacza, że każda cząstka (atom) w komórce symulacyjnej posiada dokładne odpowiedniki w każdej z otaczających komórek. W ten sposób, kiedy któryś atom opuszcza komórkę symulacyjną, jest natychmiast zastępowany przez inny, obdarzony tą samą prędkością, który przechodzi do komórki symulacyjnej z sąsiedniej komórki po drugiej stronie. Dzięki temu liczba atomów w komórce symulacyjnej pozostaje stała. Ponadto, atomy nie czują wpływu sił powierzchniowych, które w tym porządku są nieobecne.
Najważniejszymi elementami symulacji DM są potencjał oddziaływania dla wyznaczania sił działających w układzie molekuł oraz równanie ruchu zarządzające dynamiką molekuł. Potencjał oddziaływania jest zdefiniowany przez pole siłowe mechaniki molekularnej, do którego wyrażenia wchodzą człony energii potencjalnej związanej ze zmianą długości wiązań chemicznych, zmianą kątów, zmianą kątów torsyjnych, a także ze zmianami w oddziaływaniach niewiążących takich jak oddziaływania elektrostatyczne oraz van der Waalsa. Do wyrażenia na pole siłowe mogą również wchodzić różne człony mieszane. DM stosuje prawa mechaniki klasycznej – ruch każdego atomu w układzie jest opisywany klasycznym równaniem ruchu Newtona w postaci miai = Fi, gdzie i oznacza i-ty atom w układzie.
Podstawowy przebieg symulacji DM wygląda następująco: na początku definiowane są położenia (zwykle na podstawie rozwiązanej struktury krystalograficznej) oraz prędkości atomów (w oparciu o rozkład Boltzmanna). Następnie wyznaczany jest potencjał oddziaływania pomiędzy atomami oraz rozwiązywane równania ruchu dla wszystkich atomów w układzie w krótkim kroku czasowym. Na koniec kroku czasowego obliczane są pożądane wielkości fizyczne oraz współrzędne atomów są zapisywane do pliku z trajektorią. Następuje sprawdzenie czy symulacja osiągnęła zakładany czas? Jeśli nie, następuje przejście do kolejnego kroku czasowego, jeśli tak, następuje zakończenie symulacji.
Środowisko symulacji
Kompletne środowisko fizjologiczne naturalnych procesów z udziałem cząsteczek białka nie jest dostępne przy pomocy symulacji DM; zazwyczaj, najlepsze przybliżenie warunków fizjologicznych uzyskuje się prowadząc symulacje cząsteczek białka w roztworze wodnym (z udziałem lub bez udziału jonów). Modele solwatacyjne używane w symulacjach dzielą się na dyskretne, ciągłe oraz hybrydowe. W modelach dyskretnych występują bezpośrednio cząsteczki wody. W tej grupie wyróżnia się modele trzy-, cztero- i pięciopunktowe. W modelach trzypunktowych ładunki 2 atomów wodoru i atomu tlenu są zlokalizowane bezpośrednio na atomach (modele SPC, SPC/E, TIP3P), w modelach czteropunktowych ładunek atomu tlenu jest zlokalizowany na fikcyjnym atomie uplasowanym na dwusiecznej kąta HOH nieopodal właściwego atomu tlenu (modele PPC, TIP4P), zaś w modelach pięciopunktowych ładunek atomu tlenu jest zlokalizowany w miejscach dwóch wolnych par elektronowych tego atomu (model TIP5P). Modele cztero- i pięciopunktowe mają na celu poprawę charakterystyki oddziaływań elektrostatycznych molekuły wody w stosunku do modeli tradycyjnych (trzypunktowych). W modelach ciągłych takich jak model Poissona-Boltzmanna (PB) oraz uogólniony model Borna (GB) i jego warianty, rozpuszczalnik jest traktowany jako polaryzowalny ośrodek ciągły posiadający właściwości dielektryczne wody (cząsteczki wody nie występują bezpośrednio). W modelach hybrydowych cząsteczki wody są obecne bezpośrednio w obszarze przylegającym do „substancji rozpuszczonej”, natomiast w pozostałej części układu woda modelowana jest jako ośrodek ciągły. W modelach hybrydowych czasami obecna jest warstwa dodatkowa spełniająca rolę buforu pomiędzy obszarem wewnętrznym z cząsteczkami wody i zewnętrznym z wodą modelowaną jako ośrodek ciągły. Warstwa ta charakteryzuje się zmienną wartością przenikalności dielektrycznej.
Skale czasowe symulacji
Biomolekuły wykazują szeroki zakres skal czasowych związanych z przebiegiem procesów w nich bądź z ich udziałem zachodzących. W odniesieniu do białek przykładowe dynamiczne procesy i związane z nimi przybliżone skale czasowe obejmują: ruchy lokalne w zakresie nanosekundowym (ruchy łańcuchów bocznych i ruchy pętli w białkach), ruchy ciała sztywnego w zakresie nano- do mikrosekundowym (ruchy helis, ruchy domen i ruchy podjednostek w białkach) oraz ruchy na dużą skalę w zakresie mikro- do milisekundowym lub dłuższym (zmiany skrętów helis, dysocjacja/asocjacja, zwijanie i rozwijanie białek). Symulacje powinny spełniać kompromis, a więc być zaprojektowane tak aby mogły się kończyć w rozsądnym, obliczalnym czasie rzeczywistym, a zarazem, by czas symulacji był dostatecznie długi by zmieścił się w nim badany proces. Szybko wzrastająca moc komputerów, stosowanie superkomputerów, prowadzenie obliczeń w trybie równoległym oraz ostatnio implementacje algorytmów symulacyjnych na procesorach GPU (Graphical Process Unit) są najważniejszymi przyczynami stałego wzrostu czasów symulacji DM w ostatnich latach. Obecnie, najdłuższe czasy symulacji klasycznej DM, pozwalające w sprzyjających przypadkach na „zmieszczenie” procesów zwijania białek (np. fałdowanie zbudowanego z 36 aminokwasów białka Villin Headpiece w roztworze wodnym obserwowane w symulacjach DM w czasie 5.6-8.2 μs) osiągają zakresy mikro-, lub nawet – jeszcze sporadycznie – milisekundowe.
Zalety dynamiki molekularnej
Dynamika molekularna dostarcza szczegółowej informacji na poziomie cząsteczkowym i atomowym. Swobodny rozwój symulacji gwarantuje niezależność zbieranych informacji od istniejących hipotez badawczych. Informacje uzyskane na podstawie trajektorii DM pozwalają opisać ewolucję czasową badanego układu, dostarczając wiedzy na temat zmian konformacyjnych, dynamicznych oraz odnoszących się do termodynamiki obserwowanych procesów.
Metody pochodne/stowarzyszone
Obliczenia energii swobodnej
Miarą stabilności dowolnego układu jest jego energia swobodna. W szczególności, miarą stabilności kompleksu pomiędzy receptorem białkowym oraz ligandem jest energia swobodna wiązania ligandu do receptora, która ma decydujące znaczenie dla oceny wyników dokowania molekularnego używanego rutynowo w projektowaniu leków. Energia swobodna wiązania jest związana z wyznaczanym eksperymentalnie powinowactwem do wiązania albo inaczej stałą asocjacji kompleksu wedle formuły: ΔGbind = -RT ln(Ka), gdzie R – stała gazowa, T – temperatura, Ka – stała asocjacji równa ilorazowi stężenia kompleksu EI do stężeń wolnych składników E oraz I.
Energia swobodna wiązania może być obliczana z użyciem wielu różnych metod opartych o symulacje DM, które można podzielić na dwie grupy: 1. tzw. metody alchemiczne, wykorzystujące formalizm termodynamiki statystycznej, które charakteryzują się zwiększoną dokładnością, a zarazem są kosztowne obliczeniowo, takie jak metoda zaburzeń energii swobodnej (Free Energy Perturbation; FEP) i całkowanie termodynamiczne (Thermodynamic Integration; TI) oraz 2. metody przybliżone, nie tak dokładne lecz mniej wymagające obliczeniowo, takie jak liniowe przybliżenie energii oddziaływania (Linear Interaction Energy; LIE), Molecular Mechanics-Poisson-Boltzmann/Generalized Born Surface Area (MM-PB/GBSA) i szereg innych.
Zaletą metod FEP i TI są bardzo dokładne energie swobodne. Mankamentem jest wyczerpujące próbkowanie konformacyjne oraz powolna zbieżność obliczeń; w związku z tym obecne zastosowanie tych metod jest w praktyce ograniczone do niewielkich przeobrażeń strukturalnych, a więc stosunkowo blisko spokrewnionych związków. Powyższe ograniczenie nie dotyczy metod LIE i MM-PB/GBSA, które jednak nie są tak dokładne jak metody alchemiczne.
Mechanika kwantowa/mechanika molekularna (QM/MM)
Reakcje chemiczne podczas których występuje formowanie nowych lub zrywanie istniejących wiązań oraz inne procesy które pociągają za sobą zmiany w strukturze elektronowej układów mogą być badane jedynie przy użyciu metod mechaniki kwantowej. Aby umożliwić modelowanie reaktywnych układów biomolekularnych z możliwie dobrą dokładnością, utrzymując przy tym koszt obliczeniowy na zrównoważonym poziomie, wydzielony obszar chemicznie reaktywny (np. substrat i kofaktor w reakcji enzymatycznej) jest traktowany przy użyciu metody mechaniki kwantowej, zaś całe otoczenie tego obszaru, czyli reszta układu (np. całe białko i rozpuszczalnik) – przy użyciu pola siłowego mechaniki molekularnej (Rysunek 2).
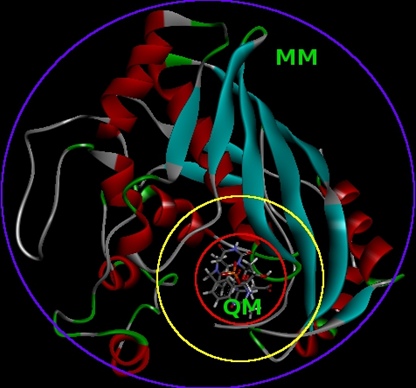
Rysunek 2. Wewnątrz czerwonego okręgu jest strefa QM traktowana przy użyciu metody mechaniki kwantowej; pomiędzy okręgami żółtym i niebieskim jest obszar MM traktowany przy użyciu pola siłowego mechaniki molekularnej; pomiędzy okręgami czerwonym i żółtym znajduje się opcjonalna warstwa buforująca obszary QM (od zewnątrz) i MM (od wewnątrz)
Całkowita energia układu jest obliczana bądź wg schematu subtraktywnego bądź addytywnego (odpowiednio, przez odjęcie energii MM dla strefy QM lub wysumowanie poszczególnych energii dla wszystkich stref). Propagacja układu przebiega przy użyciu klasycznej DM, bądź dynamiki Monte-Carlo lub Car-Parinello.
Sterowana DM
Sterowana DM wprowadza zależną od czasu lub położenia siłę, która stymuluje ruch układu wzdłuż określonych, pożądanych stopni swobody. Pozwala to badaczowi skoncentrować się na interesujących z jego punktu widzenia zdarzeniach o charakterze dynamicznym (np. siła zewnętrzna może przyspieszać wystąpienie zdarzenia polegającego na związaniu substratu lub uwolnieniu produktu) przy jednoczesnej redukcji kosztów obliczeniowych. Metoda jest użyteczna w przypadkach które nie mogą być zbadane za pomocą klasycznej DM, takich gdy badany układ podlega dużym zmianom strukturalnym i towarzyszącym im silnym zaburzeniom równowagowym.
Przyspieszona (akcelerowana) DM
Metoda akcelerowanej DM wprowadza specjalny potencjał (w znaczeniu dodatkowej energii) w sytuacji kiedy energia potencjalna układu jest poniżej określonego progu, w ten sposób znacząco zwiększając tempo przejść pomiędzy kolejnymi stanami układu.
Essential Dynamics (inaczej Principal Component Analysis czyli Analiza Głównego Składnika)
Metoda essential dynamics umożliwia obliczanie głównych kierunków ruchu układu, wyodrębnionych spośród ogółu zarejestrowanych w tym układzie ruchów. Polega to na określeniu kolektywnych drgań o niskich częstościach i dużych amplitudach, tzw. ruchów kolektywnych, dotyczących np. fragmentów drugorzędowych struktury białka. Analiza korelacji wyodrębnionych ruchów kolektywnych może pozwolić objaśnić ich znaczenie funkcjonalne, tj. znaczenie dla procesów przebiegających w badanym układzie.
Oprogramowanie
Spośród wielu pakietów oprogramowania do dynamiki molekularnej na wyróżnienie zasługują m.in.: Amber, CHARMM, GROMACS, GROMOS, NAMD, Tinker oraz Desmond. Szczegółową listę oprogramowania do modelowania molekularnego (włączając dynamikę molekularną) wraz z krótkimi charakterystykami można znaleźć na stronie:
http://www.click2drug.org/index.html#Docking
Dynamika molekularna w projektowaniu leków
Symulacje DM są zdolne do scharakteryzowania na poziomie atomowym sposobu wiązania pomiędzy receptorem białkowym oraz ligandem, uwzględniając zmiany w strukturze receptora towarzyszące wiązaniu ligandu oraz zmianę konformacji ligandu. Typową strategię projektowania leków przy użyciu modelowania komputerowego, z dynamiką molekularną jako metodą podstawową, można scharakteryzować na przykładzie projektowania analogu peptydu Shepherdin jako inhibitora białka szoku cieplnego Hsp90: 1) zostały przeprowadzone symulacje DM celem zdefiniowania dominującej konformacji peptydu Shepherdin, 2) dominująca konformacja peptydu Shepherdin została dokowana do centrum aktywnego Hsp90, 3) przeprowadzono analizę najważniejszych oddziaływań w kompleksie, 4) utworzono farmakofor (model opisujący relacje przestrzenne pomiędzy elementami wspólnymi dla ligandów oddziałujących z określonym receptorem), 5) w oparciu o farmakofor zaprojektowano małocząsteczkowy analog peptydu Shepherdin jako potencjalny nowy inhibitor Hsp90, 6) zbadano oddziaływanie zaprojektowanego inhibitora z Hsp90. Efektem takiej i podobnych procedur jest uzyskiwanie nowych związków wiodących (lead compounds) w projektowaniu leków.
Ciekawe i unikalne zastosowania DM przydatne w projektowaniu leków obejmują m.in. identyfikację utajnionych miejsc wiążących i centrów allosterycznych. Utajnione miejsca wiążące to miejsca nieoczywiste, nieidentyfikowalne z użyciem struktur pochodzenia eksperymentalnego, a więc krystalograficznych lub z NMR, odszukiwane dopiero w następstwie intensywnego próbkowania konformacyjnego przy pomocy DM. Z kolei centra allosteryczne to miejsca, do których mogą przyłączać się cząsteczki tzw. modulatorów (inhibitory, aktywatory), w wyniku czego następuje zmiana konformacji cząsteczki białka i jej aktywności biologicznej. Innym atutem DM użytecznym w projektowaniu leków jest umożliwienie lepszej identyfikacji cząsteczek ligandów dobrze wiązanych przez receptor – jest to tzw. schemat kompleksu podlegającego relaksacji. Podejście polega na modelowaniu elastyczności receptora białkowego przez uwzględnienie wielu nowych, dodatkowych jego konformacji uzyskanych z użyciem symulacji DM. Uzupełnienie typowej procedury dokowania ligandów używanej w projektowaniu leków, gdzie receptor jest zazwyczaj reprezentowany przez pojedynczą strukturę białka pozyskaną metodami eksperymentalnymi, o wiele dodatkowych konformacji białka pozwala często na identyfikowanie dodatkowych inhibitorów, wiązanych specyficznie przez ten receptor. Kolejnym atrybutem metod opartych na DM, który będzie nabierać coraz większego znaczenia w projektowaniu leków, są dokładne energie swobodne wiązania ligandu do receptora obliczane z użyciem technik alchemicznych, takich jak wspomniane wcześniej FEP i TI. Metody te wymagają bardzo szczegółowego próbkowania konformacyjnego i związanych z tym długich czasów symulacji, wobec czego nie są w tej chwili szeroko stosowane, jednak w sytuacji postępów w algorytmach i zasobach komputerowych ich znaczenie i wykorzystanie będzie rosnąć.
Końcowe uwagi/wnioski
Przez ostatnie dekady DM wyrosła jako centralna metoda w badaniach różnorodnych układów molekularnych, w tym ważnych biologicznie kompleksów pomiędzy receptorami białkowymi i małymi cząsteczkami inhibitorów, znajdując rosnącą ilość zastosowań w wielu obszarach naukowych, m.in. w chemii, biochemii oraz chemii medycznej. Wraz z postępem w metodologii i zasobach komputerowych, symulacje DM wykazują tendencję do systematycznego „rozrostu”, który należy rozumieć zarówno jako włączanie do symulacji coraz większych układów (obecnie do rzędu setek milionów atomów) oraz prowadzenie symulacji na coraz dłuższym dystansie czasowym (obecnie do zakresu milisekundowego). DM odgrywa ważną rolę we wspomaganym komputerowo projektowaniu leków (Computer-Aided Drug Design; CADD). Wynika to z faktu, iż symulacje DM potrafią odtwarzać z dużą dokładnością dynamikę wielu procesów biologicznych takich jak tworzenie kompleksu enzym (receptor)-inhibitor (ligand) czy też charakteryzować zmiany konformacyjne w aktywowanych cząsteczkach receptorów. Funkcjonalność DM zwiększa się jeśli jest ona używana (zazwyczaj jako metoda podstawowa) w kombinacji z innymi technikami modelowania komputerowego, jak np. dokowanie molekularne, obliczenia energii swobodnej, obliczenia kwantowo-mechaniczne, essential dynamics, etc.. Głównym problemem klasycznej DM jest dotarcie do tych rejonów w przestrzeni konformacyjnej, które dostępne są jedynie w wyniku pokonania barier energetycznych, albowiem próbkowanie takich stanów jest w praktyce nieosiągalne w temperaturach pokojowych. Innym ważnym problemem jest jakość pól siłowych, a w szczególności niedostatek ogólnie akceptowanych polaryzacyjnych pól siłowych, a więc takich które uwzględniałyby efekt przepływu chmur elektronowych, oraz brak dopracowanej parametryzacji dla wielu ligandów.
Literatura
1. Borhani, D.W., Shaw, D.E. (2012) The future of molecular dynamics simulations in drug discovery. J. Comput. Aided Mol. Des. 26: 15-26.
2. Salsbury Jr., F.R. (2010) Molecular dynamics simulations of protein dynamics and their relevance to drug discovery. Curr. Opin. Pharmacol. 10: 738-744.
3. Durrant, J.D., McCammon, J.A. (2011) Molecular dynamics simulations and drug discovery. BMC Biology 9: 71-79.
4. Kerrigan, J.E. (2013) Molecular dynamics simulations in drug design. Methods Mol. Biol. 993: 95-113.
5. Rastelli, G. (2013) Emerging topics in structure-based virtual screening. Pharm. Res. 30: 1458-1463.
6. Mobley, D.L., Klimovich, P.V. (2012) Perspective: Alchemical free energy calculations for drug discovery. J. Chem. Phys. 137: 230901-230912.
7. Freddolino, P.L., Schulten, K. (2009) Common structural transitions in explicit-solvent simulations of Villin Headpiece folding. Biophys. J. 97: 2338-2347.
8. Morra, G., Meli, M., Colombo, G. (2008) Molecular dynamics simulations of proteins and peptides: from folding to drug design. Curr. Protein Pept. Sci. 9: 181- 196.

